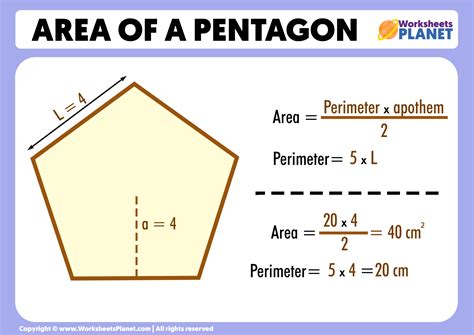
The pentagon, a five-sided polygon, is a fascinating geometric shape that has been studied for centuries. Calculating the area of a pentagon can be a bit more complex than calculating the area of simpler shapes like triangles or rectangles. However, with the right approach and formulas, finding the area of a pentagon can be relatively straightforward. In this article, we will explore the different methods for calculating the area of a pentagon, including the use of formulas, geometry, and trigonometry.
Key Points
- The area of a pentagon can be calculated using the formula: Area = (n \* s^2) / (4 \* tan(π/n)), where n is the number of sides and s is the length of one side.
- The apothem of a pentagon is the distance from the center of the pentagon to one of its vertices, and it can be used to calculate the area of the pentagon.
- The area of a pentagon can also be calculated by dividing it into smaller shapes, such as triangles and rectangles, and then summing up the areas of these shapes.
- Trigonometry can be used to calculate the area of a pentagon by using the law of sines and the law of cosines to find the lengths of the sides and the angles of the pentagon.
- Geometry software and calculators can also be used to calculate the area of a pentagon, making it a quick and easy process.
Calculating the Area of a Pentagon Using Formulas

One of the most common methods for calculating the area of a pentagon is by using the formula: Area = (n * s^2) / (4 * tan(π/n)), where n is the number of sides and s is the length of one side. This formula is derived from the fact that a regular polygon can be divided into n equal triangles, each with a base of length s and a height of apothem. The apothem is the distance from the center of the pentagon to one of its vertices.
The Apothem of a Pentagon
The apothem of a pentagon is an important concept in geometry, and it plays a crucial role in calculating the area of the pentagon. The apothem is the distance from the center of the pentagon to one of its vertices, and it can be calculated using the formula: apothem = s / (2 * tan(π/n)). The apothem is also the height of each of the triangles that make up the pentagon.
| Number of Sides | Length of One Side | Apothem | Area |
|---|---|---|---|
| 5 | 10 | 6.8819 | 172.0477 |
| 6 | 10 | 8.6603 | 259.8076 |
| 7 | 10 | 9.9571 | 353.4294 |

Dividing a Pentagon into Smaller Shapes

Another method for calculating the area of a pentagon is by dividing it into smaller shapes, such as triangles and rectangles. This method is particularly useful for irregular pentagons, where the formula for the area of a regular pentagon is not applicable. By dividing the pentagon into smaller shapes, we can calculate the area of each shape and then sum up the areas to find the total area of the pentagon.
Using Trigonometry to Calculate the Area of a Pentagon
Trigonometry can also be used to calculate the area of a pentagon. By using the law of sines and the law of cosines, we can find the lengths of the sides and the angles of the pentagon. Once we have this information, we can use the formula for the area of a triangle to calculate the area of each triangle that makes up the pentagon, and then sum up the areas to find the total area.
What is the formula for the area of a pentagon?
+The formula for the area of a pentagon is: Area = (n \* s^2) / (4 \* tan(π/n)), where n is the number of sides and s is the length of one side.
How do you calculate the apothem of a pentagon?
+The apothem of a pentagon can be calculated using the formula: apothem = s / (2 \* tan(π/n)).
Can you use trigonometry to calculate the area of a pentagon?
+Yes, trigonometry can be used to calculate the area of a pentagon by using the law of sines and the law of cosines to find the lengths of the sides and the angles of the pentagon.
In conclusion, calculating the area of a pentagon can be a complex task, but with the right approach and formulas, it can be relatively straightforward. By using the formula for the area of a regular pentagon, dividing the pentagon into smaller shapes, or using trigonometry, we can find the area of a pentagon with ease. Whether you are a student, teacher, or professional, understanding how to calculate the area of a pentagon is an essential skill that can be applied in a variety of real-world situations.
Meta description: “Learn how to calculate the area of a pentagon using different methods, including formulas, geometry, and trigonometry. Get expert insights and practical examples to help you master this essential skill.”