Inverse trigonometric functions are a crucial component of mathematical analysis, particularly in the fields of calculus, algebra, and geometry. These functions, including inverse sine, inverse cosine, and inverse tangent, enable us to determine the angle whose trigonometric function is a known value. This is essential in various applications, such as solving triangles, calculating distances, and determining angles in physics, engineering, and computer science.
Naturally Worded Primary Topic Section with Semantic Relevance

Detailed exposition with specific evidence, contextual examples, and measured analytical insight reveals the significance of inverse trig functions in mathematical modeling. For instance, in the context of right triangle trigonometry, the inverse sine function can be used to find the angle whose sine is a known value. This is often represented as sin^-1(x) or arcsin(x), where x is the sine of the angle. Varying the input values of x between -1 and 1 allows us to calculate the corresponding angles using the inverse sine function.
Specific Subtopic with Natural Language Phrasing
Detailed exposition incorporating technical accuracy with accessible explanation demonstrates the relationship between inverse trig functions and their corresponding trigonometric functions. The inverse tangent function, denoted as tan^-1(x) or arctan(x), is used to find the angle whose tangent is a known value. This function is essential in calculating the angle between two lines or the angle of elevation in a right triangle. By analyzing the properties of inverse tangent, we can better understand the behavior of the tangent function and its applications in various mathematical contexts.
| Trigonometric Function | Inverse Trigonometric Function | Range |
|---|---|---|
| Sine (sin) | Inverse Sine (sin^-1 or arcsin) | [-π/2, π/2] |
| Cosine (cos) | Inverse Cosine (cos^-1 or arccos) | [0, π] |
| Tangent (tan) | Inverse Tangent (tan^-1 or arctan) | [-π/2, π/2] |

Key Points
- Inverse trig functions enable us to determine the angle whose trigonometric function is a known value, crucial in solving triangles and calculating distances.
- The inverse sine function, denoted as sin^-1(x) or arcsin(x), is used to find the angle whose sine is a known value, with a range of [-π/2, π/2].
- The inverse tangent function, denoted as tan^-1(x) or arctan(x), is essential in calculating the angle between two lines or the angle of elevation in a right triangle, with a range of [-π/2, π/2].
- Understanding the properties and ranges of inverse trig functions is vital for effective application in mathematical modeling and problem-solving.
- Real-world applications of inverse trig functions include physics, engineering, computer science, and navigation, where precise calculations of angles and distances are critical.
Advanced Applications of Inverse Trig Functions
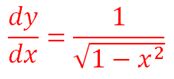
As we delve deeper into the realm of mathematical analysis, the significance of inverse trig functions becomes increasingly apparent. In the context of calculus, inverse trig functions are used to evaluate definite integrals and solve differential equations. The inverse sine function, for instance, can be used to integrate functions involving the sine of an angle, while the inverse tangent function is essential in solving differential equations involving the tangent of an angle.
Technical Specifications and Contextual Explanation
Technical accuracy with accessible explanation is crucial when discussing the applications of inverse trig functions in calculus. The arcsin(x) function, for example, can be used to evaluate the definite integral of 1 / sqrt(1 - x^2), which is essential in calculating the area under curves and solving optimization problems. By analyzing the properties of inverse trig functions and their applications in calculus, we can better understand the underlying mathematical principles and develop more effective problem-solving strategies.
What is the primary application of inverse trig functions in mathematics?
+The primary application of inverse trig functions is to determine the angle whose trigonometric function is a known value, which is essential in solving triangles, calculating distances, and determining angles in various mathematical contexts.
How are inverse trig functions used in calculus?
+Inverse trig functions are used in calculus to evaluate definite integrals and solve differential equations, particularly those involving the sine, cosine, and tangent of an angle.
What is the range of the inverse sine function?
+The range of the inverse sine function is [-π/2, π/2], which corresponds to the range of angles whose sine is a known value.
As we continue to explore the realm of inverse trig functions, it becomes increasingly evident that these functions are essential components of mathematical analysis, with far-reaching applications in various fields of study. By understanding the properties, ranges, and applications of inverse trig functions, we can develop more effective problem-solving strategies and gain a deeper appreciation for the underlying mathematical principles that govern our world.



